Problématique de la corrélation d'images
Introduction
L'appariement des images est une discipline de la vision par ordinateur qui revêt une importance dans un grand nombre d'applications pratiques. Pour n'en citer que quelques-uns, la correspondance des images est utilisée pour résoudre les problèmes de contrôle des processus industriels, reconnaissance automatique des plaques d'immatriculation dans les garages de stationnement, les phénomènes de croissance biologique, la cartographie géologique, la vision stéréoscopique, la compression vidéo et les robots autonomes pour l'exploration spatiale.
Comme les applications sont variées, il existe une grande variété d'approches et d'algorithmes utilisés aujourd'hui, beaucoup spécialisés à une tâche donnée. Par exemple, des algorithmes hautement spécialisés existent pour déterminer les vecteurs de mouvement de petites particules de traceur utilisées dans l'étude de les écoulements de fluide.
La corrélation des images numériques ne fait pas exception et des algorithmes sont utilisés qui prennent en compte la physique des processus de déformation. En raison des minuscules mouvements souvent intéressants pour les applications d'ingénierie, les exigences de résolution sont beaucoup plus élevés que pour la plupart des autres applications. Pour mesurer avec précision la courbe de contrainte-déformation pour de nombreux matériaux d'ingénierie, les changements de longueur de l'ordre de 10-5 m/m doivent être résolus.
Ces exigences ont conduit au développement de nombreux algorithmes visant à fournir une haute résolution en minimisant les erreurs.
The Correspondence Problem
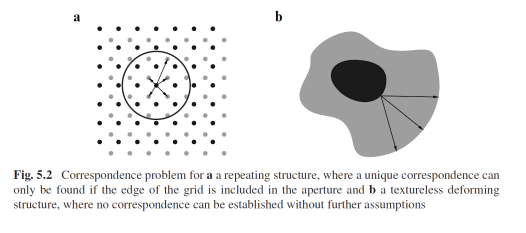
Il existe de nombreuses situations dans lesquelles une correspondance unique entre les caractéristiques de deux images ne peut pas être établies. Deux cas sont illustrés dans la Figure ci-dessous. Pour une répétition de structure telle qu'une grille de petits points, le mouvement ne peut être résolu que jusqu'à un multiple inconnu de la constante de la grille. Quand l'ensemble de la grille est considérée en augmentant la taille de l'ouverture, le problème de correspondance à nouveau devient unique et les vecteurs de mouvement peuvent être résolus.
Le problème de correspondance devient encore plus difficile à résoudre si nous le faisons ne pas se limiter à un mouvement rigide, mais considérer les cas où l'objet subit une déformation. Pour une structure sans texture subissant une déformation, nous ne pouvons obtenir aucune information de mouvement dans ses limites, car aucune caractéristique n'est présente. Mais en raison de la déformation, il est même impossible de déterminer les vecteurs de mouvement sur les limites de la structure.
solution speckle pattern
Pour résoudre le problème de correspondance de manière unique, la surface de l'objet doit présenter certaines propriétés. La discussion du problème d'ouverture ci-dessus a montré que les structures orientées telles que les lignes limitent la détermination des vecteurs de mouvement à la composante orthogonale à la structure. La texture de surface idéale devrait donc être isotrope, c'est-à-dire qu'il ne devrait pas avoir une orientation préférée. De plus, nous avons montré que répéter des textures peut conduire à des problèmes de mauvais repérage. Dans l'idéal la texture de surface doit donc être non périodique.
Ces exigences mènent naturellement à l'utilisation de textures aléatoires, telles que le motif de speckle formé quand une lumière cohérente éclaire la surface à travers une ouverture. Les modèles couramment appliqués ressemblent généralement à des modèles de mouchetures laser dans une certaine mesure. Cependant, les modèles utilisés en corrélation d'image numérique adhèrent à la surface et se déforment avec la surface, et par conséquent, aucune perte de corrélation ne se produit même sous des translations et des déformations importantes.
Quelques exemples de motifs illustrés ci-dessous. Une des clés des bons modèles de speckle sont leur contenu élevé en informations. La surface est texturée, les informations pour la correspondance de motif sont disponibles partout sur
la surface, et pas seulement sur une grille relativement clairsemée. Cela permet l'utilisation d'une ouverture relativement petite pour la correspondance de motif, communément appelée un sous-ensemble ou fenêtre (subset).
