Corrélation : complément d'information
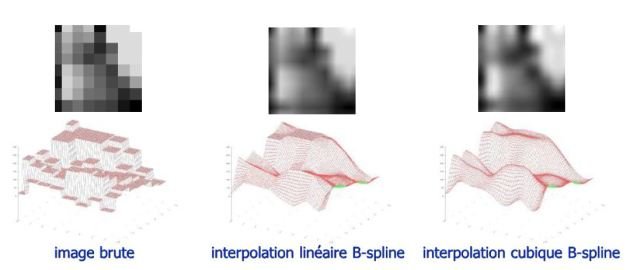
Interpolation
Déformation de l'imagette
•Cas général :
–L'imagette de l'image déformée n'est plus carrée :
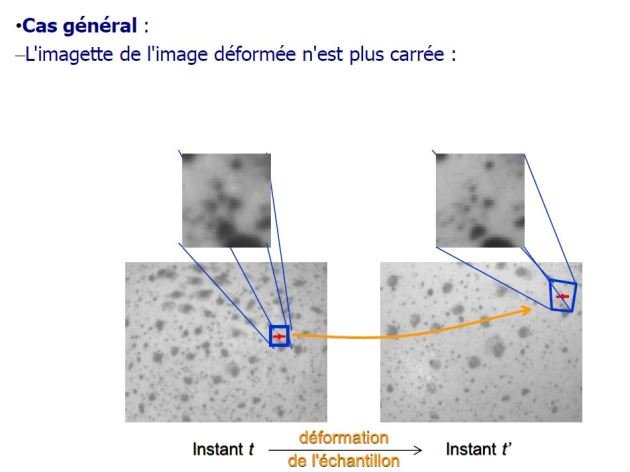
•Solution :
–modéliser ce changement de forme (fonction de forme de l'imagette) en utilisant un développement de Taylor :
Ordre 0 : 2 paramètres : translations
Ordre 1 : transformation affine, 6 paramètres = ordre 0 + rotation, homothétie, cisaillement
Order 2 : fonction quadratique, 12 paramètres = ordre 1 + courbure
Résumé
La corrélation s'exprime en fonction :
• des déplacements du centre de l'imagette u, v
• des gradients de déplacement du/dx, du/dy, dv/dx, dv/dy
C = f(u, v, du/dx, du/dy, dv/dx, dv/dy)
Algorithme de corrélation
– première boucle
• traiter toutes les imagettes
• pour chacune, définir un pointage initial pour initialiser la deuxième boucle
– deuxième boucle
• démarrer l'optimisation à partir du pointage initial
• optimiser la fonction de corrélation (trouver le meilleur emplacement de l'imagette déformée en interpolant entre les pixels)
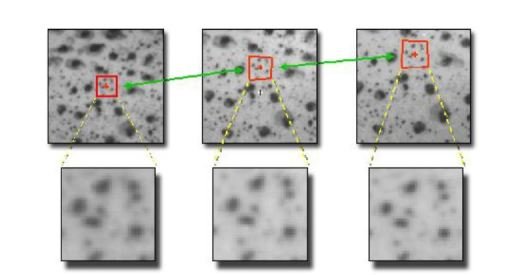
• Les résultats du traitement d'une imagette sont utilisés pour initialiser le traitement de l'imagette voisine (propagation spatiale)
• Les résultats du traitement d'une image sont utilisés pour initialiser le traitement de l'image suivante (propagation temporelle)
• Les propagations spatiale et temporelle des calculs emploient avantageusement les méthodes prédictives (extrapolation, filtrage Kalman etc.)
• Pour une imagette donnée de l'image de référence, le logiciel considère les emplacements les plus probables de l'imagette correspondante dans l'image déformée, en se basant sur :
– l'emplacement des imagettes les plus proches déjà calculées (propagation spatiale)
– l'emplacement de cette même imagette dans les calculs précédents (propagation temporelle)
• L'appariement des imagettes par le programme peut être considéré comme une minimisation énergétique :
– un appariement minimise l'énergie totale, somme des différences quadratiques des différences entre les niveaux de gris des deux imagettes (critère SSD)
Conditions d'éclairage
• Pendant l'acquisition des images :
– les conditions d'éclairage peuvent changer
– des réflexions peuvent survenir si la pièce se déforme
– les temps d'exposition peuvent varier
– la luminance de l'échantillon peut changer en fonction de ses déformations
– la peinture du mouchetis peut se détériorer
• Il n'est jamais garanti que la “cartographie photométrique” soit homogène, d'où la possibilité que l'algorithme de corrélation donne de fausses similitudes
• Solution : modéliser la transformation photométrique pour améliorer la robustesse du calcul de corrélation
• I(x,y) = P(I*(x+u,y+v))
– I(x,y) est le niveau de gris du pixel de coordonnées (x;y) dans l'image I
– I*(x+u,y+v) est le niveau de gris du pixel de coordonnées (x+u;y+v) dans l'image transformée I*
– P est la fonction recherchée (cartographie photométrique) reliant les valeurs de niveau de gris des deux pixels correspondants
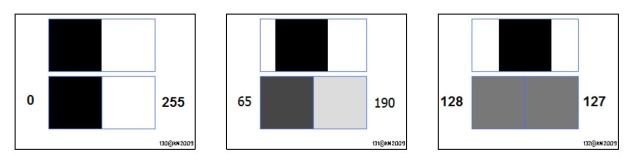
- Ordre 0 : simple décalage de niveau, P(z) = z + b Défini comme le critère NSSD (Normalized Sum of Squared Differences) Correction des variations d'éclairement
- Ordre 1 : pente et décalage de niveau, P(z) = az + b Défini comme le critère ZNSSD (Zero Normalized Sum of Squared Differences) Correction des variations d'éclairement et de contraste
SSD : Sum of Squared Differences. Ce critère ne prend pas du tout en compte les changements de luminosité et ne doit pas être utilisé en général. Son usage est réservé aux situations avec de faibles contrastes, quand les autres critères peuvent se révéler inefficaces.
NSSD : Normalized Sum of Squared Differences. Ce critère prend en compte un facteur d'échelle d'éclairage. Il est généralement très robuste et adapté à la plupart des applications.
ZNSSD : Zero-normalized sum of squared differences. Ce critère tient compte à la fois d'un facteur d'échelle et d'un décalage des niveaux de gris. Il est recommandé en cas de changements importants de luminosité ou quand les bits significatifs des valeurs transmises changent. Peut se montrer inapproprié en cas d'images peu contrastées.
Interpolation
Déformations
• On obtient les déformations en dérivant le champ de déplacement (calcul de gradient)
• Un modèle polynomial permet le calcul des dérivées : u(x, y) = u0 + ux x + uy y v(x, y) = v0 + vx x + vy y
• Calcul des déformations de Green-Lagrange :
εxx = ux + 0,5(ux2+vx2)
εyy = vy + 0,5(uy2+vy2)
εxy = 0,5(uy+vx)
En chaque point de calcul, les déformations sont calculées à partir des valeurs u et v des 4 points voisins