Moyens métrologiques avancés

Bien qu'il soit relativement simple pour un observateur humain d'identifier le mouvement dans les images, il n'est pas simple de formuler le problème en termes mathématiques, et en effet, de nombreuses approches différentes existent. Dans cette section, nous allons présenter une ou deux méthodes basiques (suivant le temps disponible).

Pour illustrer le problème de l'estimation du mouvement, nous considérons un problème unidimensionnel, comme illustré à la Fig. ci-dessous. Soit G (x, t) la distribution d'intensité sur l'objet en fonction du temps.

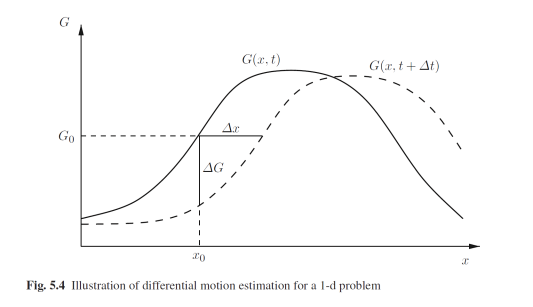
Si le mouvement est suffisamment petit, on peut approcher la valeur de gris autour d'un point d'intérêt par un développement de Taylor du premier ordre

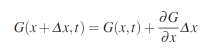
Si l'objet se déplace à une vitesse constante constant u', une valeur de gris sera déplacée par un quantité Δ x = u'Δt dans un intervalle de temps Δt et la distribution des valeurs de gris après un pas de temps Δt est simplement une copie décalée de la distribution de la valeur de gris d'origine

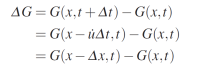
En combinant les deux équations précédentes, nous pouvons exprimer le changement de la valeur de gris ΔG en fonction de la pente de l'intensité comme suit:

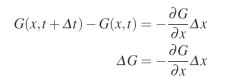
ET donc obtenir une estimation pour le déplacement :

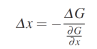
Pour les petits mouvements, le déplacement est donc donné par le changement d'intensité divisé par la pente du motif d'intensité. En substituant Δ x = ˙ uΔt dans l'équation précédente, nous pouvons obtenir une estimation de la vitesse

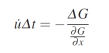
Et en prenant la limite lorsque Δt tend vers 0 on arrive à :

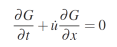
Pour la vitesse bidimensionnelle v, la même dérivation peut être suivie en utilisant le développement de Taylor G (x + Δx) = G (x) + Δx · ∇G, et on arrive à l'équation suivante :

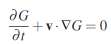
Cette équation est communément appelée équation de changement de luminosité pour le flux optique, et a été au centre d'un vaste corpus de recherches dans les décennies passées . Bien qu'une discussion approfondie des méthodes de flux optique soit hors de notre portée, nous allons discuter d'une méthode simple solution pour déterminer les déplacements en fonction de cette équation. Nous la réécrivons pour le cas discret et multiplier par le pas de temps entre les images pour obtenir :

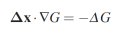
L'étude de l'équation précédente révèle qu'il est généralement impossible de déterminer un mouvement bidimensionnel sans information supplémentaire. Tout d'abord, si les gradients d'intensité sont nuls, le mouvement ne peut pas être déterminé du tout. Mais même pour des dégradés non nuls, cette équation fournit une seule équation pour deux inconnues. Comme le produit scalaire Δx · ∇G peut être écrit comme étant la magnitude du gradient multipliée par la composante de Δx orientée dans la direction du gradient de valeur de gris local, c'est-à-dire que la composante Δ⊥ est perpendiculaire au bord local, mouvement perpendiculaire au bord de la valeur grise locale

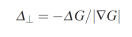
Cette limitation est une expression mathématique du problème d'ouverture décrit précédemment et peut être résolue en utilisant un petit voisinage, par exemple un sous-ensemble carré de l'image, au lieu d'un seul point. En supposant que le mouvement est à peu près constant sur un petit voisinage, on peut écrire  cette équation pour une collection de N points à proximité du point d'intérêt pour donner le système suivant :

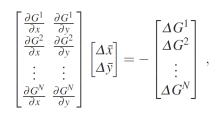
Pour plus de deux points, il s'agit d'un système d'équations surdimensionné de la forme :

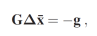
qui peut être résolu pour le mouvement moyen Δ¯x au sens des moindres carrés par

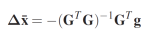
Ou sous forme d'un système en prenant les deux directions :

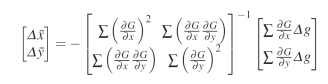
le mouvement peut être estimé tant que la matrice G.transposée(G) n'est pas singulière, c'est-à-dire

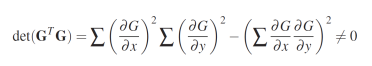
Trivialement, cela signifie que tous les dérivés de valeur grise ne doivent pas être nuls. En d'autres termes, l'estimation du mouvement n'est pas possible dans les régions de valeurs de gris constantes. De plus, le déterminant disparaîtra également si tous les gradients de valeurs de gris sont alignés dans la même direction. Dans ce cas, les dérivées partielles dans les deux directions de coordonnées sont liées par un facteur constant, et on peut facilement montrer que cela implique que le déterminant dans Eq. (5.13) disparaîtra.

Dans cette section, nous dérivons une méthode d'estimation de mouvement basée sur la minimisation de la différence de valeur de gris entre un petit sous-ensemble d'une image (modèle) et une copie déplacée sur une autre image. Nous supposons qu'entre les deux images le modèle et sa copie déplacée ne diffèrent que par un bruit aléatoire gaussien. On note l'image de référence à partir de laquelle le gabarit est pris F , et l'image après déplacement par G. On essaie maintenant de minimiser la différence au carré en valeurs de gris, dite somme de carrés (SSD), dans un voisinage

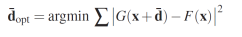
Pour résoudre le vecteur de déplacement optimal dopt, nous pouvons utiliser un algorithme itératif simple en développant notre fonction de coût dans une série de Taylor de premier ordre.

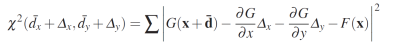
Ici, d¯x et d¯y sont les estimations actuelles du mouvement moyen du sous-ensemble, et Δx et Δy sont les mises à jour de mouvement incrémentielles recherchées dans l'itération en cours. Prendre des dérivées partielles par rapport à Δx et Δy et les mettre à zéro dans le système d'équations linéaires suivant pour les mises à jour de l'incrément dans chaque itération

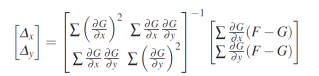
L'équation peut être utilisée pour améliorer de manière itérative l'estimation du mouvement moyen dans la nieme itération en utilisant ¯dp + 1 = ¯d p + Δ jusqu'à ce que la convergence vers le vecteur de mouvement optimal ¯dopt soit atteinte. Cette technique d'enregistrement de l'image itérative est l'algorithme de suivi Lucas – Kanade. Le tracker Lucas-Kanade est une extension de l'estimateur du mouvement différentiel dérivé dans la section précédente. L'algorithme de Lucas-Kanade n'est pas limité aux petits vecteurs de mouvement, et en effet, des mouvements arbitrairement grands peuvent être trouvés tant que l'estimation initiale est dans le rayon de convergence de la méthode.