La reconstruction
Résultat brut d'une tomographie
Le résultat d'une tomographie est un problème inverse mal posé :
• Problème inverse : On dispose de mesures et il faut trouver ce qui a produit ces mesures
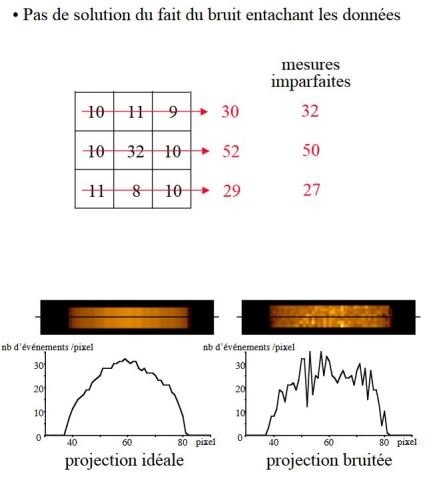
• Problème mal posé : La solution est instable : une petite différence sur les projections peut conduire à des coupes reconstruites très différentes.
Pourquoi ?
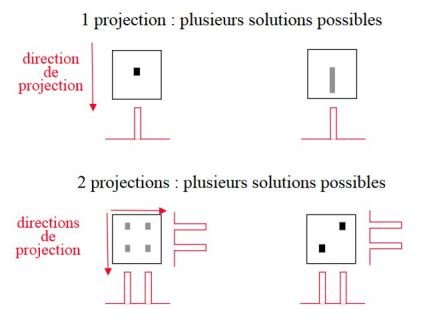
Pas de solution unique : toujours plusieurs objets compatibles avec un ensemble fini de projections.
Unicité de la solution pour une infinité de projections seulement.
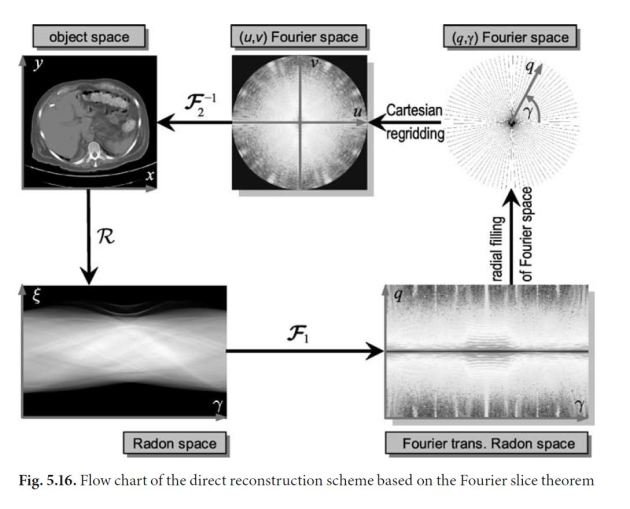
Transformée de Radon
en 1917 Johann Radon publie " De la détermination des fonctions à partir de leurs intégrales selon certaines directions". Ces travaux permettent une formulation continue de l'opérateur de projection
Le problème posé par la reconstruction tomographique est le problème inverse, il faut donc inverser la transformée de Radon,c'est à dire estimer f(x,y) à partir de p(u,θ).
La représentation des projections dans l'espace de radon s'appelle un sinogramme. Un sinogramme représente une ligne vue sous les différents angles de mesures. Il y a donc un sinogramme par ligne. Les sinogrammes et les projections contiennent les mêmes informations ils différent juste sur la manière de les représenter.
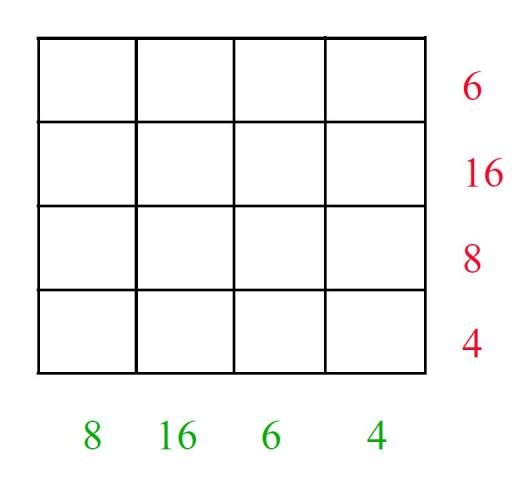
Exemple : Avez vous compris ?
On dispose de 64 projections de dimension 128 pixels (dans la direction axiale ) x 256 pixels
Combien de coupes transaxiales peut-on reconstruire ?
Combien de sinogrammes peut-on former à partir de ces projections ?
Quelles sont les dimensions d'un sinogramme ?
Exemple : Réponses
On dispose de 64 projections de dimension 128 pixels (dans la direction axiale ) x 256 pixels
Combien de coupes transaxiales peut-on reconstruire ?
128 coupes
Combien de sinogrammes peut-on former à partir de ces projections ?
128
Quelles sont les dimensions d'un sinogramme ?
64*256
Exemple : Exemple 1
Est-ce une projection ou un sinogramme ?
Exemple : Exemple 2
Si toutes les projections sont identiques à celles-ci, quel est le sinogramme correspond à la coupe indiquée ?
Exemple : Réponse exemple 2
Exemple : Exemple 3
A quoi correspond ce sinogramme ?
Exemple : Réponse Exemple 3
De nombreuses méthodes de reconstruction
Analytiques, discrètes, rapides il y a de nombreuses méthodes de reconstruction plus ou moins rapides plus ou moins performantes. une des plus classique :
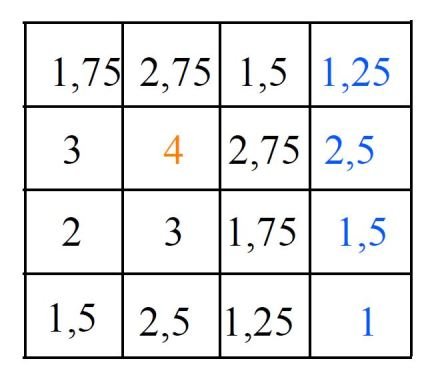
Exemple : Exemple de la rétro-projection filtrée
La première opération qui peut être mise en œuvre est la rétro-projection. Elle correspond à la valeur moyenne de toutes les projections sur chaque point de l'objet à l'emplacement correspondant.
Exemple : BFP par l'exemple
